▲
top
top
Pythonでマンデルブロ集合(Mandelblot set)をプロットしたい
マンデルブロ集合のプロット
1. プログラム全文
2. 使い方
3. 実行結果
4. tanhを用いた発散速度のプロットについて
5. n次の複素数の計算について
6. 長さが無限である様子を確認する
このページではこのような






0. マンデルブロ集合とは
マンデルブロ集合とは、漸化式 Z(x+1) = Z(x)^2 + C , Z(0) = 0 があった時、xをどんどん大きくしていく。その結果 Z(x) が無限大に発散しないような複素数 C の集合である。 またこの集合には数学的に面白い性質があり、円のように閉じた図形でありながら周の長さは無限である。その様子もこのページで紹介しようと思う。
具体的に C = 0 の時、
Z(0) = 0
Z(1) = Z(0)^2 + 0 = 0
Z(2) = Z(1)^2 + 0 = 0
Z(100) = 0
このように無限大には発散しないので C = 0 はマンデルブロ集合に含まれる。Z(1) = Z(0)^2 + 0 = 0
Z(2) = Z(1)^2 + 0 = 0
Z(100) = 0
次に C = 1 の時は、
Z(0) = 0
Z(1) = Z(0)^2 + 1 = 1
Z(2) = Z(1)^2 + 1 = 2
Z(3) = 2^2 + 1 = 5
Z(4) = 5^2 + 1 = 26
Z(5) = 677
Z(6) = 458,330
Z(7) = 210,066,388,901
このように Z(x) の値がどんどん大きくなっていき、最終的には無限大に発散する。よって C = 1 はマンデルブロ集合には含まれない。Z(1) = Z(0)^2 + 1 = 1
Z(2) = Z(1)^2 + 1 = 2
Z(3) = 2^2 + 1 = 5
Z(4) = 5^2 + 1 = 26
Z(5) = 677
Z(6) = 458,330
Z(7) = 210,066,388,901
まず方針として、調べたい範囲内の全ての座標において無限大に発散するかどうかを計算し、発散したかしなかったかをプロットする。 また、発散する速度を加味してプロットした方が美しい図形になるので発散速度によるヒートマップを描くことにする。
説明は後回しにして、作成したプログラムと使い方と実行結果を紹介する。
1. プログラム全文
class mandelblot:
import matplotlib.pyplot as plt, numpy as np, math
def __init__(self, n:int=2, pixel:int=200, xy_range=[[-2.1, 0.5], [-1.2, 1.2]], count_type:int=0, is_add=True):
self.n = n
self.xy_range = xy_range
self.count_type = count_type
self.is_add = is_add
xs = self.np.linspace(xy_range[1][0], xy_range[1][1], pixel+1)
ys = self.np.linspace(xy_range[0][0], xy_range[0][1], pixel+1)
self.xy = [[self.calc(r, i) for i in xs] for r in ys]
self.xs = [xs for y in ys]
self.ys = [[y for _ in ys] for y in ys]
def combination(self, a, b):
result = 1
for i in range(b):
result *= (a-i)/(b-i)
return result
def i_separate(self, k):
result = self.math.sin(self.math.radians(k*90 + 45))
if(result < 0):
return -1
elif (result > 0):
return 1
return 0
def comp_binomial(self, r, i, n):
real, imagine, add = 0., 0., 0.
for k in range(n+1):
if(k % 2 == 0):
num = self.combination(n, k)*(i**k)*(r**(n-k))*self.i_separate(k)
real += num
add += self.absol(num)
else:
imagine += self.combination(n, k)*(i**k)*(r**(n-k))*self.i_separate(k)
#print(real, imagine)
return real, imagine, add
def absol(self, n):
return n if(n >= 0) else -n
def calc(self, r, i, lim=1e6, for_range=2**7):
new_r, new_i, add = 0., 0., 0.
for count in range(for_range):
try:
new_r, new_i, add = self.comp_binomial(new_r + r, new_i + i, self.n)
except :
return self.scale(count)
if(self.is_add):
if(add >= lim):
return self.count_scale(count)
else:
if(new_r >= lim):
return self.count_scale(count)
return -1
def count_scale(self, n):
"""
count_typeの説明
0 : 発散速度をそのまま反映 <- 基本
1 : 発散速度を2乗 <- 集合の正確さが高くなる
2 : tanh(円周率/発散速度) <- 発散速度の分布が見やすい。
3 : 発散の有無のみを反映(発散すれば1, しなければ-1)
"""
if(self.count_type == 0):
return n
elif(self.count_type == 1):
return n**2
elif (self.count_type == 2):
if(n == 0):
return 0
else:
return self.math.tanh(self.math.pi/n)
elif (self.count_type == 3):
return 1 if(n > 0) else -1
else:
return n
def s_g_scale(self, s_g):
s = s_g[0][1] - s_g[0][0]
g = s_g[1][1] - s_g[1][0]
return s, g
def plot(self, size=10, save=False, axis=True, buff=""):
s, g = self.s_g_scale(self.xy_range)
fig = self.plt.figure(figsize=(size*s, size*g))
self.plt.pcolor(self.ys, self.xs, self.xy)
if not(axis):
self.plt.axis("off")
self.plt.show()
if(save):
fig.savefig("mandelblot"+buff+".jpg")
import matplotlib.pyplot as plt, numpy as np, math
def __init__(self, n:int=2, pixel:int=200, xy_range=[[-2.1, 0.5], [-1.2, 1.2]], count_type:int=0, is_add=True):
self.n = n
self.xy_range = xy_range
self.count_type = count_type
self.is_add = is_add
xs = self.np.linspace(xy_range[1][0], xy_range[1][1], pixel+1)
ys = self.np.linspace(xy_range[0][0], xy_range[0][1], pixel+1)
self.xy = [[self.calc(r, i) for i in xs] for r in ys]
self.xs = [xs for y in ys]
self.ys = [[y for _ in ys] for y in ys]
def combination(self, a, b):
result = 1
for i in range(b):
result *= (a-i)/(b-i)
return result
def i_separate(self, k):
result = self.math.sin(self.math.radians(k*90 + 45))
if(result < 0):
return -1
elif (result > 0):
return 1
return 0
def comp_binomial(self, r, i, n):
real, imagine, add = 0., 0., 0.
for k in range(n+1):
if(k % 2 == 0):
num = self.combination(n, k)*(i**k)*(r**(n-k))*self.i_separate(k)
real += num
add += self.absol(num)
else:
imagine += self.combination(n, k)*(i**k)*(r**(n-k))*self.i_separate(k)
#print(real, imagine)
return real, imagine, add
def absol(self, n):
return n if(n >= 0) else -n
def calc(self, r, i, lim=1e6, for_range=2**7):
new_r, new_i, add = 0., 0., 0.
for count in range(for_range):
try:
new_r, new_i, add = self.comp_binomial(new_r + r, new_i + i, self.n)
except :
return self.scale(count)
if(self.is_add):
if(add >= lim):
return self.count_scale(count)
else:
if(new_r >= lim):
return self.count_scale(count)
return -1
def count_scale(self, n):
"""
count_typeの説明
0 : 発散速度をそのまま反映 <- 基本
1 : 発散速度を2乗 <- 集合の正確さが高くなる
2 : tanh(円周率/発散速度) <- 発散速度の分布が見やすい。
3 : 発散の有無のみを反映(発散すれば1, しなければ-1)
"""
if(self.count_type == 0):
return n
elif(self.count_type == 1):
return n**2
elif (self.count_type == 2):
if(n == 0):
return 0
else:
return self.math.tanh(self.math.pi/n)
elif (self.count_type == 3):
return 1 if(n > 0) else -1
else:
return n
def s_g_scale(self, s_g):
s = s_g[0][1] - s_g[0][0]
g = s_g[1][1] - s_g[1][0]
return s, g
def plot(self, size=10, save=False, axis=True, buff=""):
s, g = self.s_g_scale(self.xy_range)
fig = self.plt.figure(figsize=(size*s, size*g))
self.plt.pcolor(self.ys, self.xs, self.xy)
if not(axis):
self.plt.axis("off")
self.plt.show()
if(save):
fig.savefig("mandelblot"+buff+".jpg")
2. 使い方
プロットは二行で終わる。
① m = mandelblot()
② m.plot()
また、それぞれオプションを追加できる。
① m = mandelblot(
n = マンデルブロ集合 : Z(x)^n + C の n の値,
pixel = 整数で、どれだけ細かい座標まで計算するのかの値,
xy_range = [[xの開始値, 終了値], [yの開始値, 終了値]],
count_type = 発散速度をどのようにプロットするのか。0〜3までの数字で指定。後に説明,
is_add = 発散したかどうかの判定を実部の絶対値で行うか否か。True か False
)
count_type = 0 で発散速度をそのまま反映
count_type = 1 で(発散速度)^2 : 集合の正確さが上がる。
count_type = 2 で双曲線関数tanh(π/発散速度) : 発散速度の分布が見やすい。
count_type = 3 で発散したかどうかのみを反映
② m.plot(
size = 画像サイズの単位。実際にはsizeの値 * xyの最大値と最小値の差が画像サイズ,
save = 画像を保存するか否か。True か False,
axis = 縦軸・横軸をプロットするか否か。True か False,
buff = 画像の保存名に付け足す文字列
)
① m = mandelblot()
② m.plot()
また、それぞれオプションを追加できる。
① m = mandelblot(
n = マンデルブロ集合 : Z(x)^n + C の n の値,
pixel = 整数で、どれだけ細かい座標まで計算するのかの値,
xy_range = [[xの開始値, 終了値], [yの開始値, 終了値]],
count_type = 発散速度をどのようにプロットするのか。0〜3までの数字で指定。後に説明,
is_add = 発散したかどうかの判定を実部の絶対値で行うか否か。True か False
)
count_type = 0 で発散速度をそのまま反映
count_type = 1 で(発散速度)^2 : 集合の正確さが上がる。
count_type = 2 で双曲線関数tanh(π/発散速度) : 発散速度の分布が見やすい。
count_type = 3 で発散したかどうかのみを反映
② m.plot(
size = 画像サイズの単位。実際にはsizeの値 * xyの最大値と最小値の差が画像サイズ,
save = 画像を保存するか否か。True か False,
axis = 縦軸・横軸をプロットするか否か。True か False,
buff = 画像の保存名に付け足す文字列
)
3. 実行結果
m.plot(size=20)

m.plot(size=20)

2次から10次までのマンデルブロ集合:
g = 0.5 if(i > 2) else 0
m = mandelblot(n=i, pixel=500, count_type=2, xy_range=[[-2+g, 1+g], [-1.5, 1.5]])
m.plot(size=20, save=True, buff=str(i))
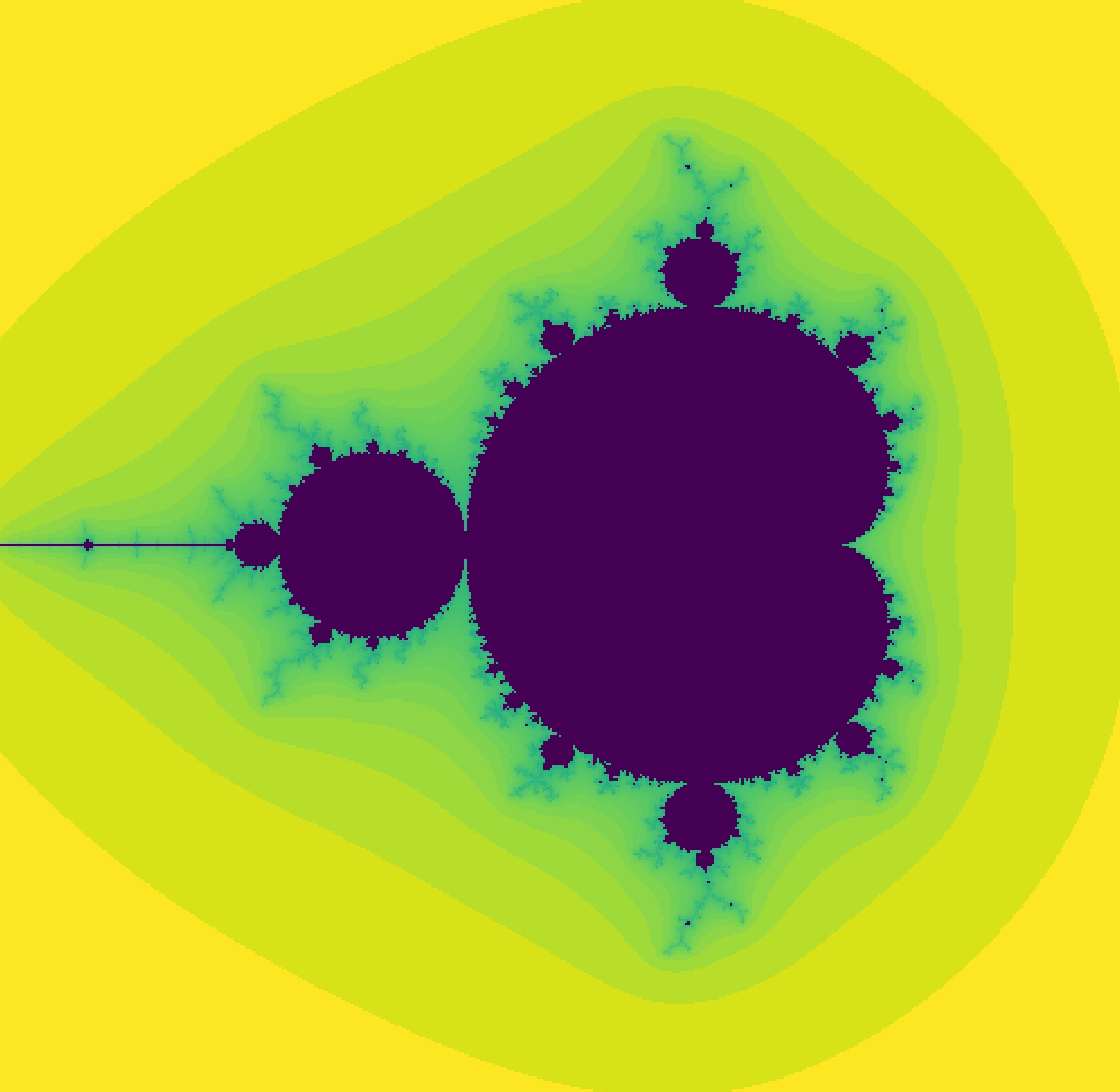








もっと高画質の画像が必要ならば pixel か size の値を上げて実行すれば良い。
4. tanhを用いた発散速度のプロットについて
このプログラムにて発散速度のプロットにtanh(π/発散速度)を用いた。これは早期に発散した数値を誇張して表示させるためである。 発散速度の計測はcalc()関数にて Z(x) の値を x=0 から 10^6 までの範囲で計算して、無限大に発散した際の x を配列に保存することで出している。 しかし、実際に計算してみると発散した x の値のほとんどは 10 以下であり、0 ~ 10^6 までの尺度でプロットするとその細かい数値の差が潰れてしまう。
そこで双曲線関数tanhを用いることにした。
y = tanh(x) のグラフ -> 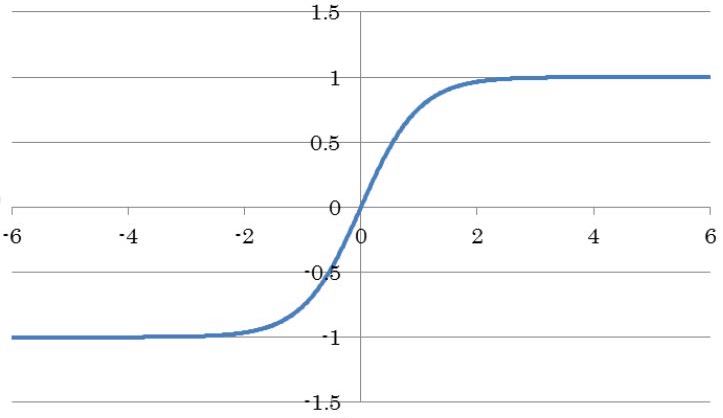
このtanhはニューラルネットワークの活性化関数としても活躍するもので、y=-1 と y=1 に漸近し、x=0 付近の傾きが大きい。この関数を用いることで大きい数字を排除して小さい変化を観察することができる。
実際に y = tanh(π/x) のグラフを x=1 ~ 100 まででプロットしてみる。

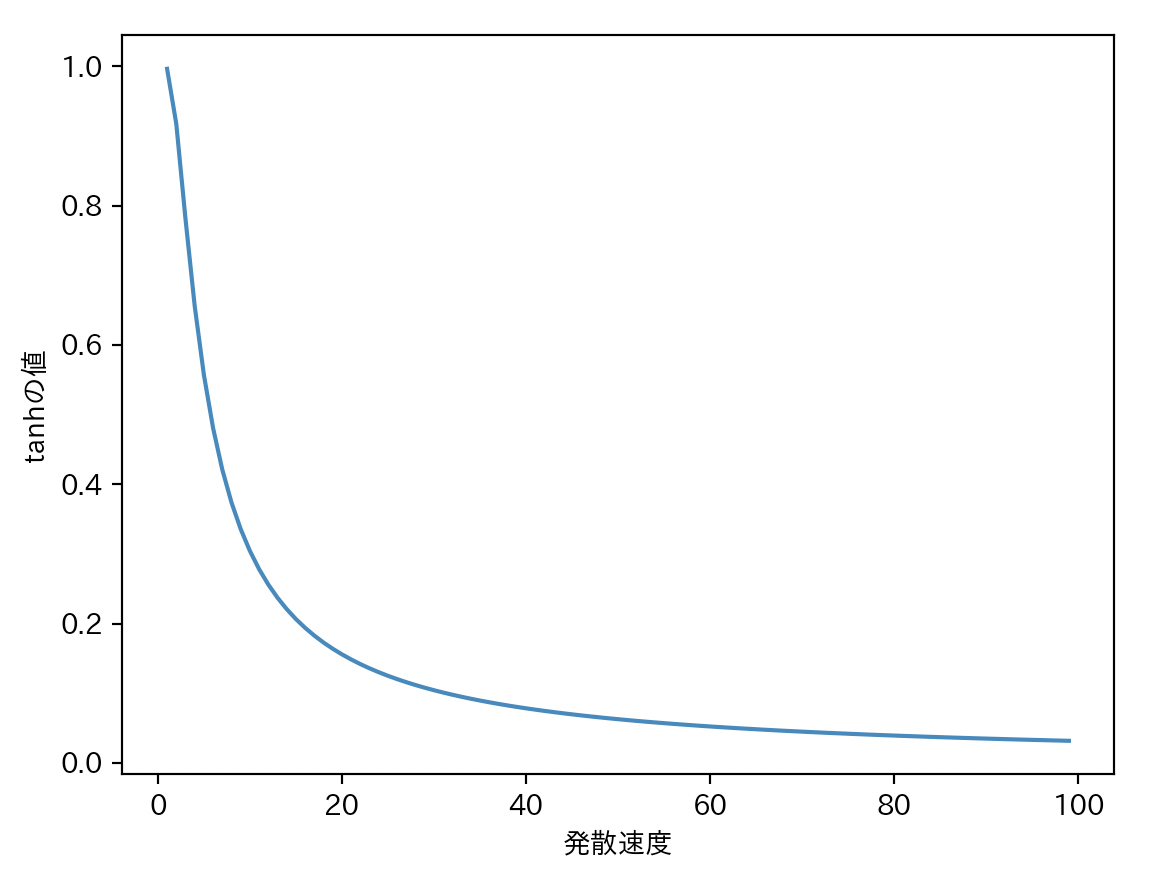
5. n次の複素数の計算について
n次のマンデルブロ集合の計算は、複素数 (a + bi)^n + C の計算の反復によって行われている。 (a + b)^n の計算には二項定理を用いることができるが、二項定理を複素数に適応しようとすると実部と虚部を分けたり、虚数 i の累乗の正負を判定したりしなくてはならないので少し複雑になる。 詳しくは別の記事複素数の二項定理についてをご参照いただきたい。 簡単に説明すると、複素数の積をベクトルの積として考え、その三角関数がとる値から計算している。
6. 長さが無限である様子を確認する
最初に言った通り、この図形の周の長さは無限である。それを確認するために計算する範囲を小さくして拡大してみる。



このようにどんなに拡大しても端っこが見えないし、拡大した先に更に同じ形のマンデルブロ集合があるように見える。 これが「周の長さが無限」の意味である。
さいごに
マンデルブロ集合のような複素数における発散点の集合を「発散点集合(Escaping set)」と呼び、その中でも反復的で長さが無限大のものを「フラクタル」と呼ぶ。 この集合には他に、ジュリア集合やバーニングシップ集合などがある。 式がわかればプログラムでプロットすることができるので興味があれば試すのも良い暇つぶしになりそうである。
マンデルブロ集合のような複素数における発散点の集合を「発散点集合(Escaping set)」と呼び、その中でも反復的で長さが無限大のものを「フラクタル」と呼ぶ。 この集合には他に、ジュリア集合やバーニングシップ集合などがある。 式がわかればプログラムでプロットすることができるので興味があれば試すのも良い暇つぶしになりそうである。
にっきのページに戻る