▲
top
top
Pythonで複素数の実部と虚部について考え、二項定理を計算したい
複素数の二項定理について
はじめに
以前、マンデルブロ集合をプロットした(該当ページ)際に複素数に二項定理を使わなければならない場面があった。 今回はその際に書いたコードを共有しようと思う。
以前、マンデルブロ集合をプロットした(該当ページ)際に複素数に二項定理を使わなければならない場面があった。 今回はその際に書いたコードを共有しようと思う。
このページでは、二項定理を使って複素数 (a+bi)^n を計算し、実部と虚部に分けて出力するところまでを行う。
完成したコードまで読み飛ばす
二項定理とは高校数学で登場する↓これのことである。
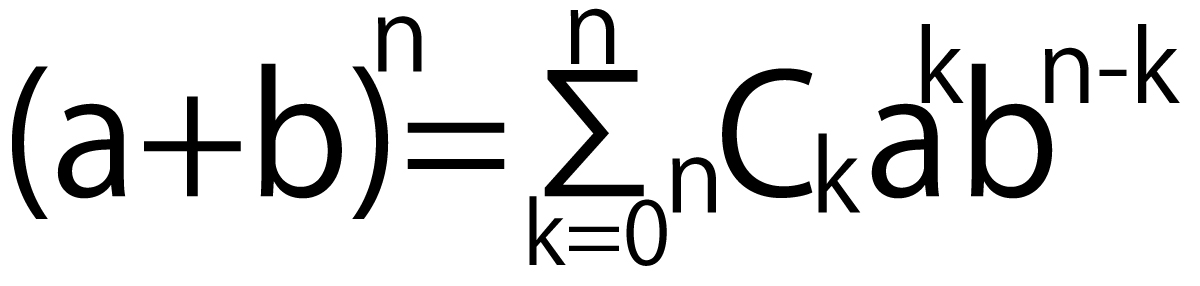
これをそのまま実装することは容易い。
def combination(a, b):
result = 1
for i in range(b):
result *= (a-i)/(b-i)
return result
def binomial(a, b, n):
result = 0
for k in range(n+1):
result += combination(n, k)*(b**k)*(a**(n-k))
result = 1
for i in range(b):
result *= (a-i)/(b-i)
return result
def binomial(a, b, n):
result = 0
for k in range(n+1):
result += combination(n, k)*(b**k)*(a**(n-k))
combination(3, 2) と入力すれば 3C2 を計算してくれる。
binomial(3, 5, 2) と入力すれば (3+5)^2 を計算してくれる。
これで (a+b)^n は計算できるようになったが、(a+bi)^n を同じように計算するには実部と虚部を分けて計算する必要がある。
一応Pythonには虚数が実装されており、虚数単位 i は complex(-1**1/2) で表される。しかしこの complex() はint型やfloat型との加減乗除の計算が不可能であり、かつ実部と虚部を切り離すことができない。 そのため二項定理の計算に落とし込むことができないので、別の方法を考える。
まず、二項定理の計算途中での実部になる条件と虚部になる条件を考える。
i^2 = -1 であるため、(bi)^n について n が偶数ならば実部になり、奇数ならば虚部になるので下のようなアルゴリズムが成り立つ。
(a+bi)^n に対して
for k in range(n+1):
if( k が偶数):
実部 += nCk * b^k * a^(n-k) * i^k
if( k が奇数):
虚部 += nCk * b^k * a^(n-k) * i^k
for k in range(n+1):
if( k が偶数):
実部 += nCk * b^k * a^(n-k) * i^k
if( k が奇数):
虚部 += nCk * b^k * a^(n-k) * i^k
次に i^k の計算である。虚数の指数計算は単純ではなく i^2 = -1 に対して i^4 = 1 である通り、正負に注意する必要がある。 これは複素数平面が縦横の尺度ではなく角度と原点からの距離(半径)の二つの尺度を持つことに関係している。ここで、複素数平面におけるベクトルの積を考える。
複素数平面上の点 (a, bi) は三角関数を用いて ( r*cos(t), i*r*sin(t) ) と表される(r は半径でr=√(a^2+b^2), t は角度)。
これを用いて (a+bi)^k を求める。
a+bi = r*( cos(t) + i*sin(t) )
(a+bi)^2 = a^2 + 2abi - b^2
= r^2*cos^2(t) + 2*b*cos(t)*b*sin(t)*i - b^2*sin^2(t)
= r^2*( cos^2(t) - sin^2(t) + i*2sin(t)cos(t) )
= r^2*( cos(2t) + i*sin(2t) )
(a+bi)^3 = a^3 + 3a^2*bi - 3ab^2 - b^3*i
= ・・・
= r^3*( cos(3t) + i*sin(3t) )
(a+bi)^4 = a^4 + 4a^3*bi - 6a^2*b^2 - 4ab^3*i + b^4
= ・・・
= r^4*( cos(4t) + i*sin(4t) )
ここまでくると法則性が見えてくる。
(a+bi)^k = r^k*( cos(k*t) + i*sin(k*t) ) ・・・ 式(1)
この式(1)の虚数部分を切り取ると i*sin(k*t) となる。
a+bi = r*( cos(t) + i*sin(t) )
(a+bi)^2 = a^2 + 2abi - b^2
= r^2*cos^2(t) + 2*b*cos(t)*b*sin(t)*i - b^2*sin^2(t)
= r^2*( cos^2(t) - sin^2(t) + i*2sin(t)cos(t) )
= r^2*( cos(2t) + i*sin(2t) )
(a+bi)^3 = a^3 + 3a^2*bi - 3ab^2 - b^3*i
= ・・・
= r^3*( cos(3t) + i*sin(3t) )
(a+bi)^4 = a^4 + 4a^3*bi - 6a^2*b^2 - 4ab^3*i + b^4
= ・・・
= r^4*( cos(4t) + i*sin(4t) )
ここまでくると法則性が見えてくる。
(a+bi)^k = r^k*( cos(k*t) + i*sin(k*t) ) ・・・ 式(1)
この式(1)の虚数部分を切り取ると i*sin(k*t) となる。
今回求めたいのは虚数部分の正負であるので、sin(k*t) の正負を確認すれば良い。
(ここから下は余談)
(a, b) = ( r*cos(t), i*r*sin(t) )の関係より
(a+bi)^k = ( r*cos(t) + i*r*sin(t) )^k
= r^k * ( cos(t) + i*sin(t) )^k
が求められる。これと式(1)を見比べると
式(1)・・・(a+bi)^k = r^k * ( cos(k*t) + i*sin(k*t) )
∴( cos(t) + i*sin(t) )^k = cos(k*t) + i*sin(k*t)
が成り立つので「ド・モアブルの定理」を導出できる。
また、式(1)が意味しているのは複素数平面上のベクトルの積は「半径は積、角度は和になる」ということである。
(a, b) = ( r*cos(t), i*r*sin(t) )の関係より
(a+bi)^k = ( r*cos(t) + i*r*sin(t) )^k
= r^k * ( cos(t) + i*sin(t) )^k
が求められる。これと式(1)を見比べると
式(1)・・・(a+bi)^k = r^k * ( cos(k*t) + i*sin(k*t) )
∴( cos(t) + i*sin(t) )^k = cos(k*t) + i*sin(k*t)
が成り立つので「ド・モアブルの定理」を導出できる。
また、式(1)が意味しているのは複素数平面上のベクトルの積は「半径は積、角度は和になる」ということである。
以上のことより、i^k における sin(k*t) の正負を求めればよいことがわかる。 i は極座標平面において i*sin(90˚) に当たるので式(1)より i^k = i*sin(k*90˚) で計算を行う。
しかしこのままでは k が偶数の時にx軸と重なってしまい正負が判定不可能になってしまうので、正負に影響しない範囲(0˚ < s < 90˚)での s を k*90˚ に足し合わせる。 ここでは適当に s = 45˚ とした。
なので実際に計算するのは sin( k*90˚ + 45˚ ) である。
def i_separate(k):
import math
result = math.sin(math.radians(k*90 + 45))
if(result < 0):
return -1
elif(result > 0):
return 1
import math
result = math.sin(math.radians(k*90 + 45))
if(result < 0):
return -1
elif(result > 0):
return 1
math.radians() は、角度をラジアンに変換する関数である。
この i_separate() 関数と前述した実部と虚部を分けて計算するアルゴリズムを用いれば複素数の二項定理を計算することができる。
それを踏まえてコードを書いた。
プログラム全文
import math
def combination(a, b):
result = 1
for i in range(b):
result *= (a-i)/(b-i)
return result
def i_separate(k):
result = math.sin(math.radians(k*90 + 45))
if(result < 0):
return -1
elif(result > 0):
return 1
def comp_binomial(r, i, n):
real, imagine = 0., 0.
for k in range(n+1):
if(k % 2 == 0):
real += combination(n, k)*(i**k)*(r**(n-k))*i_separate(k)
else:
imagine += combination(n, k)*(i**k)*(r**(n-k))*i_separate(k)
return real, imagine
def combination(a, b):
result = 1
for i in range(b):
result *= (a-i)/(b-i)
return result
def i_separate(k):
result = math.sin(math.radians(k*90 + 45))
if(result < 0):
return -1
elif(result > 0):
return 1
def comp_binomial(r, i, n):
real, imagine = 0., 0.
for k in range(n+1):
if(k % 2 == 0):
real += combination(n, k)*(i**k)*(r**(n-k))*i_separate(k)
else:
imagine += combination(n, k)*(i**k)*(r**(n-k))*i_separate(k)
return real, imagine
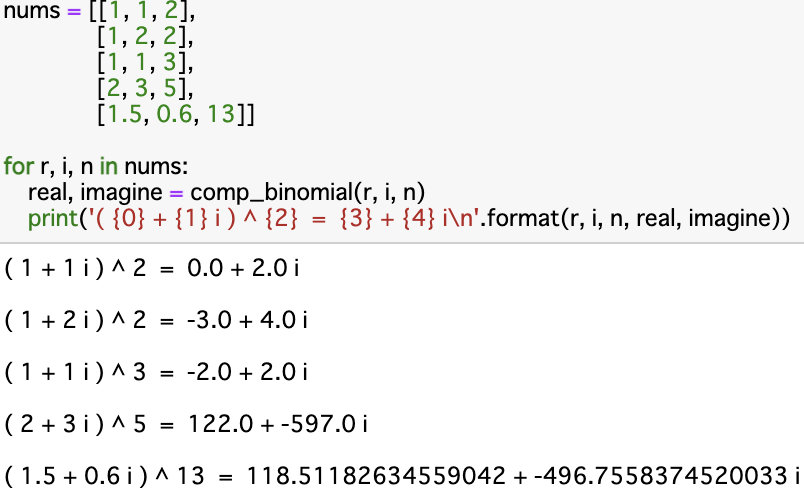
(2+3i)^4 を計算したければ comp_binomial(2, 3, 4) を実行する。その時の出力は (実部の値, 虚部の値) である。
実行してみる。
にっきのページに戻る