▲
top
top
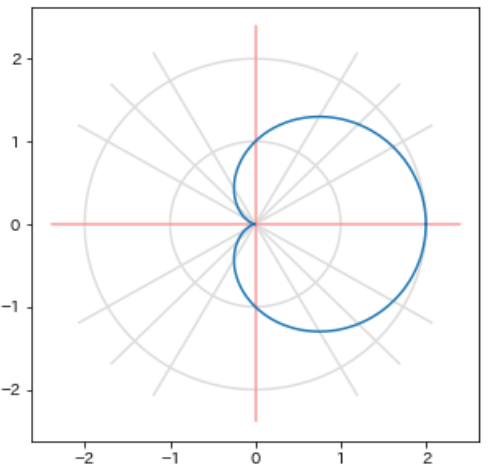
Pythonで極座標平面の図形をプロットしたい
極座標平面上の図形のプロット
完成したコードまで読み飛ばす
まず三角関数を用いて半径、角度をxy座標に変換する関数comp()を書いた。
import math
def comp( r, d ):
return r * math.cos(math.radians(d)), r * math.sin(math.radians(d))
def comp( r, d ):
return r * math.cos(math.radians(d)), r * math.sin(math.radians(d))
この関数の引数は半径(radians):r と角度(degrees):d の二つで、戻り値はx座標とy座標のタプルだ。 一方で、Pythonでのsin(90度)の計算結果は0.999...となってしまうので、小数点3桁までの絶対値で切り上げる関数rnd()を作成した。
この二つの関数を含んだクラスComplexを下記のようにした。
class Complex:
import math
def comp( self, r, d ):
return self.rnd( r * self.math.cos( self.math.radians(d) ) ), self.rnd( r * self.math.sin( self.math.radians(d) ) )
def rnd( self, n, keta=-3 ):
return ( n // 10**keta ) * 10**keta
import math
def comp( self, r, d ):
return self.rnd( r * self.math.cos( self.math.radians(d) ) ), self.rnd( r * self.math.sin( self.math.radians(d) ) )
def rnd( self, n, keta=-3 ):
return ( n // 10**keta ) * 10**keta
次に図形のプロットを実装する。
角度のみに従属する式を受け取れば、その式に0から360度までの角度を代入していくことでそれぞれの半径を求めることができる。角度と求めた半径をcomp関数でxy座標に変換すれば極座標平面上の図形をプロットできるはずである。 それを実行する関数plot()を作成した。
def plot( self, f ): # f = f(d) = r
xs, ys = [], []
for i in range( 361 ):
try:
x, y = self.comp( f( self.math.radians(i) ), i )
xs.append( x )
ys.append( y )
except:
pass
self.plt.figure( figsize=( 5, 5 ) )
self.plt.plot( xs, ys )
return None
xs, ys = [], []
for i in range( 361 ):
try:
x, y = self.comp( f( self.math.radians(i) ), i )
xs.append( x )
ys.append( y )
except:
pass
self.plt.figure( figsize=( 5, 5 ) )
self.plt.plot( xs, ys )
return None
ここまでのコードを実行し、f(d)=1のグラフをプロットしてみる。
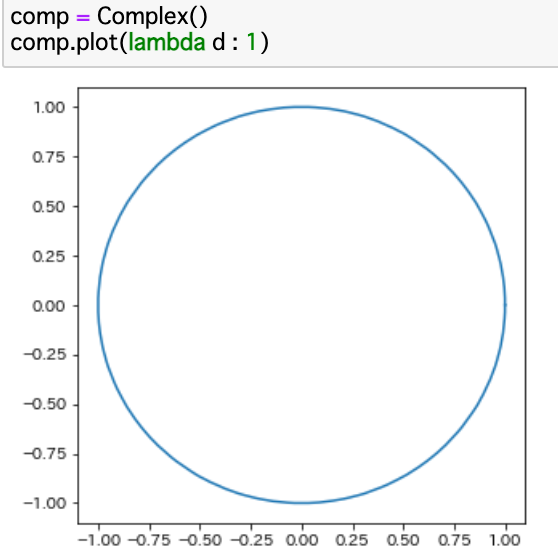
半径1の綺麗な円を描くことができた。しかしこのままでは見にくいのでグリッドを描画する。
半径を等間隔に、角度は30、45、60度などの代表角をグリッドとして描画する関数grid_plot()を作成した。x_mはx座標の最大値、y_mはy座標の最大値である。
def grid_plot( self, x_m, y_m ):
z = self.math.sqrt( x_m**2 + y_m**2 )
z_count = 0
dr = 10**(int( self.math.log( z, 10 )))
while True:
if( z_count > z ):
break
xs, ys = [], []
for i in range( 361 ):
x, y = self.comp( z_count, i )
xs.append( x )
ys.append( y )
self.plt.plot( xs, ys, c='#dddddd' )
z_count += dr
ds = [ 30, 45, 60, 120, 135, 150 ]
for d in ds:
x, y = self.comp( z, d )
self.plt.plot( [ -1*x, x ], [ -1*y, y ], c='#dddddd' )
self.plt.plot( [ 0, 0 ], [ -1*z, z ], c='#ff9999' )
self.plt.plot( [ -1*z, z ], [ 0, 0 ], c='#ff9999' )
return None
z = self.math.sqrt( x_m**2 + y_m**2 )
z_count = 0
dr = 10**(int( self.math.log( z, 10 )))
while True:
if( z_count > z ):
break
xs, ys = [], []
for i in range( 361 ):
x, y = self.comp( z_count, i )
xs.append( x )
ys.append( y )
self.plt.plot( xs, ys, c='#dddddd' )
z_count += dr
ds = [ 30, 45, 60, 120, 135, 150 ]
for d in ds:
x, y = self.comp( z, d )
self.plt.plot( [ -1*x, x ], [ -1*y, y ], c='#dddddd' )
self.plt.plot( [ 0, 0 ], [ -1*z, z ], c='#ff9999' )
self.plt.plot( [ -1*z, z ], [ 0, 0 ], c='#ff9999' )
return None
以上のコードをまとめたものは下記だ。
プログラム全文
class Complex:
import math, matplotlib.pyplot as plt, numpy as np
def comp( self, r, d ):
return self.rnd( r * self.math.cos( self.math.radians(d) ) ), self.rnd( r * self.math.sin( self.math.radians(d) ) )
def rnd( self, n, keta=-3 ):
return ( n // 10**keta ) * 10**keta
def plot( self, f ): # f = f(d) = r
xs, ys = [], []
for i in range( 361 ):
try:
x, y = self.comp( f( self.math.radians(i) ), i )
xs.append( x )
ys.append( y )
except:
pass
self.plt.figure( figsize=( 5, 5 ) )
self.grid_plot( max(xs), max(ys) )
self.plt.plot( xs, ys )
return None
def grid_plot( self, x_m, y_m ):
z = self.math.sqrt( x_m**2 + y_m**2 )
z_count = 0
dr = 10**(int( self.math.log( z, 10 )))
while True:
if( z_count > z ):
break
xs, ys = [], []
for i in range( 361 ):
x, y = self.comp( z_count, i )
xs.append( x )
ys.append( y )
self.plt.plot( xs, ys, c='#dddddd' )
z_count += dr
ds = [ 30, 45, 60, 120, 135, 150 ]
for d in ds:
x, y = self.comp( z, d )
self.plt.plot( [ -1*x, x ], [ -1*y, y ], c='#dddddd' )
self.plt.plot( [ 0, 0 ], [ -1*z, z ], c='#ff9999' )
self.plt.plot( [ -1*z, z ], [ 0, 0 ], c='#ff9999' )
return None
import math, matplotlib.pyplot as plt, numpy as np
def comp( self, r, d ):
return self.rnd( r * self.math.cos( self.math.radians(d) ) ), self.rnd( r * self.math.sin( self.math.radians(d) ) )
def rnd( self, n, keta=-3 ):
return ( n // 10**keta ) * 10**keta
def plot( self, f ): # f = f(d) = r
xs, ys = [], []
for i in range( 361 ):
try:
x, y = self.comp( f( self.math.radians(i) ), i )
xs.append( x )
ys.append( y )
except:
pass
self.plt.figure( figsize=( 5, 5 ) )
self.grid_plot( max(xs), max(ys) )
self.plt.plot( xs, ys )
return None
def grid_plot( self, x_m, y_m ):
z = self.math.sqrt( x_m**2 + y_m**2 )
z_count = 0
dr = 10**(int( self.math.log( z, 10 )))
while True:
if( z_count > z ):
break
xs, ys = [], []
for i in range( 361 ):
x, y = self.comp( z_count, i )
xs.append( x )
ys.append( y )
self.plt.plot( xs, ys, c='#dddddd' )
z_count += dr
ds = [ 30, 45, 60, 120, 135, 150 ]
for d in ds:
x, y = self.comp( z, d )
self.plt.plot( [ -1*x, x ], [ -1*y, y ], c='#dddddd' )
self.plt.plot( [ 0, 0 ], [ -1*z, z ], c='#ff9999' )
self.plt.plot( [ -1*z, z ], [ 0, 0 ], c='#ff9999' )
return None
<使い方>
まずインスタンスを生成
comp = Complex()
その後に式を入力する。
comp.plot(lambda d : dの式)
例えば半径 2 の円を描きたければ lambda d : 2 と入力すれば良い。 また、Complexクラス内にmathモジュールを用意したので、comp.math.~~ のように書けばmathモジュール内の関数を用いることができる。 詳しい例は下に添付した画像をご参照いただきたい。
まずインスタンスを生成
comp = Complex()
その後に式を入力する。
comp.plot(lambda d : dの式)
例えば半径 2 の円を描きたければ lambda d : 2 と入力すれば良い。 また、Complexクラス内にmathモジュールを用意したので、comp.math.~~ のように書けばmathモジュール内の関数を用いることができる。 詳しい例は下に添付した画像をご参照いただきたい。
実際にjupyter notebookにて実行する。
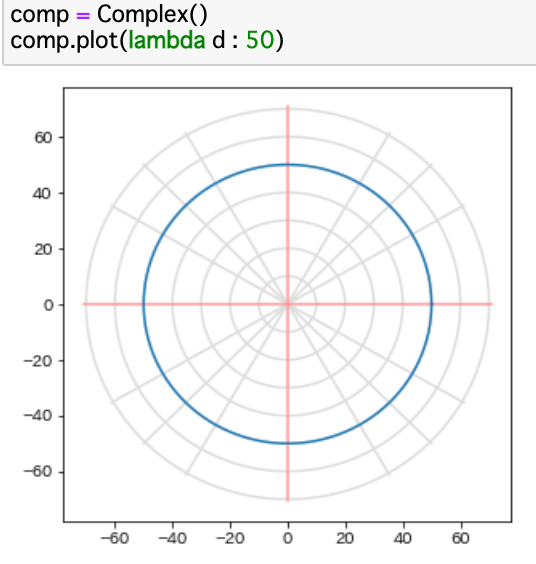
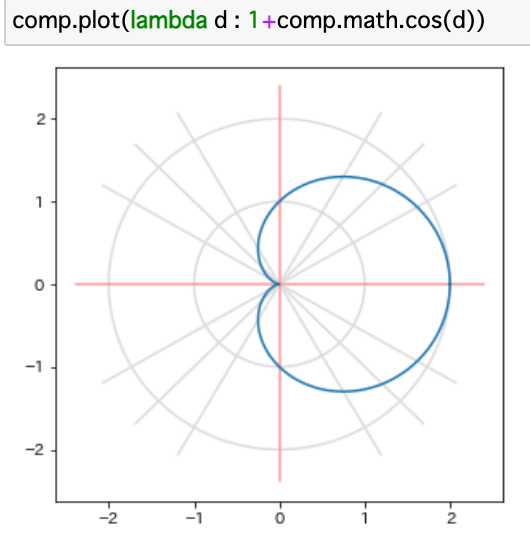
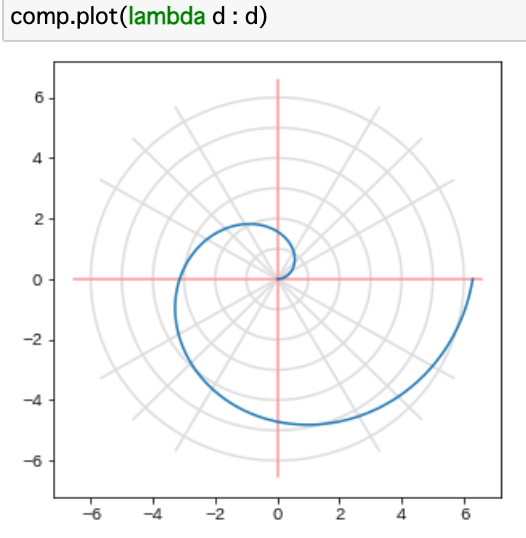
また、下に示すような面白い図形もプロットできる。
にっきのページに戻る